Euler–Bernoulli beam theory

From Wikipedia, the free encyclopedia

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.(November 2008)

Continuum mechanics

Laws[show]
Solid mechanics [hide] Solids Stress · Deformation Compatibility Finite strain · Infinitesimal strain Elasticity (linear) · Plasticity Bending · Hooke's law Failure theory Fracture mechanics Frictionless/Frictional Contact mechanics
Fluid mechanics [show]
Rheology [show]
Scientists[show]
v d e

This vibrating glass beam may be modeled as a cantilever beam with acceleration, variable linear density, variable section modulus, some kind of dissipation, springy end loading, and possibly a point mass at the free end.

Euler–Bernoulli beam theory (also known as engineer's beam theory or classical beam theory)^[1] is a simplification of the linear theory of elasticity which provides a means of calculating the load-carrying and deflection characteristics of beams. It covers the case for small deflections of a beam which is subjected to lateral loads only. It is thus a special case ofTimoshenko beam theory which accounts for shear deformation and is applicable for thick beams. It was first enunciated circa 1750,^[2] but was not applied on a large scale until the development of the Eiffel Tower and the Ferris wheel in the late 19th century. Following these successful demonstrations, it quickly became a cornerstone of engineering and an enabler of theSecond Industrial Revolution.

Additional analysis tools have been developed such as plate theory and finite element analysis, but the simplicity of beam theory makes it an important tool in the sciences, especiallystructural and mechanical engineering.

[edit]History

Schematic of cross-section of a bent beam showing the neutral axis.

Prevailing consensus is that Galileo Galilei made the first attempts at developing a theory of beams, but recent studies argue that Leonardo da Vinci was the first to make the crucial observations. Da Vinci lackedHooke's law and calculus to complete the theory, whereas Galileo was held back by an incorrect assumption he made.^[3]

The Bernoulli beam is named after Jacob Bernoulli, who made the significant discoveries. Leonhard Euler and Daniel Bernoulli were the first to put together a useful theory circa 1750.^[4] At the time, science andengineering were generally seen as very distinct fields, and there was considerable doubt that a mathematical product of academia could be trusted for practical safety applications. Bridges and buildings continued to be designed by precedent until the late 19th century, when the Eiffel Towerand Ferris wheel demonstrated the validity of the theory on large scales.

For practical purposes, such as in the European design codes, it has now been superseded by the Perry Robertson formula which takes account of initial deflection of the beam.^[5]

[edit]Static beam equation

Bending of an Euler-Bernoulli beam. Each cross-section of the beam is at 90 degrees to the neutral axis.

The Euler-Bernoulli equation describes the relationship between the beam'sdeflection and the applied load^[6]:

$\frac{\mathrm{d}^2}{\mathrm{d} x^2}\left(EI \frac{\mathrm{d}^2 w}{\mathrm{d} x^2}\right) = q.\,$

The curve

w (x)

describes the deflection

w

of the beam at some position

x

(recall that the beam is modeled as a one-dimensional object).

q

is a distributed load, in other words a force per unit length (analogous topressure being a force per area); it may be a function of

x

w

, or other variables.

Note that

E

is the elastic modulus and that

I

is the second moment of area.

I

must be calculated with respect to the centroidal axis perpendicular to the applied loading. For an Euler-Bernoulli beam not under any axial loading this axis is called the neutral axis.

Often,

w = w (x)

q = q (x)

, and EI is a constant, so that:

$EI \frac{\mathrm{d}^4 w}{\mathrm{d} x^4} = q(x).\,$

This equation, describing the deflection of a uniform, static beam, is used widely in engineering practice. Tabulated expressions for the deflection

w

for common beam configurations can be found in engineering handbooks. For more complicated situations the deflection can be determined by solving the Euler-Bernoulli equation using techniques such as the "slope deflection method", "moment distribution method", "moment area method, "conjugate beam method", "the principle of virtual work", "direct integration", "Castigliano's method", "Macaulay's method" or the "direct stiffness method".

Successive derivatives of

w

have important meanings:

$\textstyle{w}\,$ is the deflection.
$\textstyle{\frac{\mathrm{d} w}{\mathrm{d} x}} = \varphi\,$ is the slope of the beam.
$-\textstyle{EI\frac{\mathrm{d}^2 w}{\mathrm{d} x^2}} = M\,$ is the bending moment in the beam.
$\textstyle{-\frac{\mathrm{d}}{\mathrm{d} x}\left(EI\frac{\mathrm{d}^2 w}{\mathrm{d} x^2}\right)} = Q\,$ is the shear force in the beam.

The stresses in a beam can be calculated from the above expressions after the deflection due to a given load has been determined.

A number of different sign conventions can be found in the literature on the bending of beams and care should be taken to maintain consistency.^[6] In this article, the sign convention has been chosen so the coordinate system is right handed. Forces acting in the positive

x

and

z

directions are assumed positive. The sign of the bending moment is chosen so that a positive value leads to a tensile stress at the bottom cords. The sign of the shear force has been chosen such that it matches the sign of the bending moment.

[edit]Dynamic beam equation

Finite element method model of a vibration of a wide-flange beam (I-beam).

The dynamic beam equation is the Euler-Lagrange equation for the following action

$S = \int_0^L \left[ \frac{1}{2} \mu \left( \frac{\partial w}{\partial t} \right)^2 - \frac{1}{2} EI \left( \frac{ \partial^2 w}{\partial x^2} \right)^2 + q(x) w(x,t)\right] dx$

The first term represents the kinetic energy where

μ

is the mass per unit length; the second one represents the potential energy due to internal forces (when considered with a negative sign) and the third term represents the potential energy due to the external load

q (x)

. The Euler-Lagrange equationis used to determine the function that minimizes the functional

S

. For a dynamic Euler-Bernoulli beam, the Euler-Lagrange equation is

$\cfrac{\partial^2 }{\partial x^2}\left(EI\cfrac{\partial^2 w}{\partial x^2}\right) = - \mu\cfrac{\partial^2 w}{\partial t^2} + q(x)$

[show]Derivation of Euler–Lagrange equation for beams

[edit]Stress

Besides deflection, the beam equation describes forces and moments and can thus be used to describe stresses. For this reason, the Euler–Bernoulli beam equation is widely used in engineering, especially civil and mechanical, to determine the strength (as well as deflection) of beams under bending.

Both the bending moment and the shear force cause stresses in the beam. The stress due to shear force is maximum along the neutral axisof the beam (when the width of the beam, t, is constant along the cross section of the beam; otherwise an integral involving the first moment and the beam's width needs to be evaluated for the particular cross section), and the maximum tensile stress is at either the top or bottom surfaces. Thus the maximum principal stress in the beam may be neither at the surface nor at the center but in some general area. However, shear force stresses are negligible in comparison to bending moment stresses in all but the stockiest of beams as well as the fact thatstress concentrations commonly occur at surfaces, meaning that the maximum stress in a beam is likely to be at the surface.

[edit]Simple or symmetrical bending

Element of a bent beam: the fibers form concentric arcs, the top fibers are compressed and bottom fibers stretched.

For beam cross-sections that are symmetrical about a plane perpendicular to the neutral plane, it can be shown that the tensile stress experienced by the beam may be expressed as:

$\sigma = \frac{Mz}{I} = -zE ~ \frac{\mathrm{d}^2 w}{\mathrm{d} x^2}.\,$

Here,

z

is the distance from the neutral axis to a point of interest; and

M

is the bending moment. Note that this equation implies that pure bending (of positive sign) will cause zero stress at the neutral axis, positive (tensile) stress at the "top" of the beam, and negative (compressive) stress at the bottom of the beam; and also implies that the maximum stress will be at the top surface and the minimum at the bottom. This bending stress may be superimposed with axially applied stresses, which will cause a shift in the neutral (zero stress) axis.

[edit]Maximum stresses at a cross-section

Quantities used in the definition of the section modulus of a beam.

The maximum tensile stress at a cross-section is at the location

z = c 1

and the maximum compressive stress is at the location

z = - c 2

where the height of the cross-section is

h = c 1 + c 2

. These stresses are

$\sigma_1 = \cfrac{Mc_1}{I} = \cfrac{M}{S_1} ~;~~ \sigma_2 = -\cfrac{Mc_2}{I} = -\cfrac{M}{S_2}$

The quantities

S 1, S 2

are the section moduli^[6] and are defined as

$S_1 = \cfrac{I}{c_1} ~;~~ S_2 = \cfrac{I}{c_2}$

The section modulus combines all the important geometric information about a beam's section into one quantity. For the case where a beam is doubly symmetric,

c 1 = c 2

and we have one section modulus

S = I / c

[edit]Strain in an Euler–Bernoulli beam

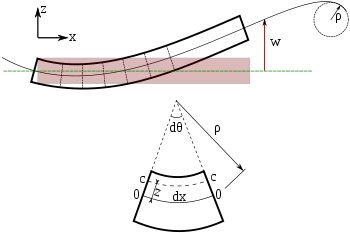
We need an expression for the strain in terms of the deflection of the neutral surface to relate the stresses in an Euler-Bernoulli beam to the deflection. To obtain that expression we use the assumption that normals to the neutral surface remain normal during the deformation and that deflections are small. These assumptions imply that the beam bends into an arc of a circle of radius

ρ

(see Figure 1) and that the neutral surface does not change in length during the deformation.^[6]

Let

d x

be the length of an element of the neutral surface in the undeformed state. For small deflections, the element does not change its length after bending but deforms into an arc of a circle of radius

ρ

. If

dθ

is the angle subtended by this arc, then $\mathrm{d}x = \rho~\mathrm{d}\theta$ .

Let us now consider another segment of the element at a distance

z

above the neutral surface. The initial length of this element is

d x

. However, after bending, the length of the element becomes $\mathrm{d}x' = (\rho-z)~\mathrm{d}\theta = \mathrm{d}x - z~\mathrm{d}\theta$ . The strain in that segment of the beam is given by

$\varepsilon_x = \cfrac{\mathrm{d}x'-\mathrm{d}x}{\mathrm{d}x} = -\cfrac{z}{\rho} = -\kappa~z$

where

κ

is the curvature of the beam. This gives us the axial strain in the beam as a function of distance from the neutral surface. However, we still need to find a relation between the radius of curvature and the beam deflection

w

[edit]Relation between curvature and beam deflection

Let P be a point on the neutral surface of the beam at a distance

x

from the origin of the

(x, z)

coordinate system. The slope of the beam, i.e., the angle made by the neutral surface with the

x

-axis, at this point is

$\theta(x) = \cfrac{\mathrm{d}w}{\mathrm{d}x}$

Therefore, for an infinitesimal element

d x

, the relation $\mathrm{d}x = \rho~\mathrm{d}\theta$ can be written as

$\cfrac{1}{\rho} = \cfrac{\mathrm{d}\theta}{\mathrm{d}x} = \cfrac{\mathrm{d}^2w}{\mathrm{d}x^2} = \kappa$

Hence the strain in the beam may be expressed as

$\varepsilon_{x} = -z\cfrac{\mathrm{d}^2w}{\mathrm{d}x^2}$

[edit]Stress-strain relations

For a one-dimensional linear elastic material, the stress is related to the strain by $\sigma = E\varepsilon$ where

E

is the Young's modulus. Hence the stress in an Euler-Bernoulli beam is given by

$\sigma_x = -zE\cfrac{\mathrm{d}^2w}{\mathrm{d}x^2}$

Note that the above relation, when compared with the relation between the axial stress and the bending moment, leads to

$M = -EI\cfrac{\mathrm{d}^2w}{\mathrm{d}x^2}$

Since the shear force is given by

Q = d M / d x

, we also have

$Q = -EI\cfrac{\mathrm{d}^3w}{\mathrm{d}x^3}$

[edit]Boundary considerations

The beam equation contains a fourth-order derivative in

x

. To find a unique solution

w (x, t)

we need four boundary conditions. The boundary conditions usually model supports, but they can also model point loads, distributed loads and moments. The support or displacement boundary conditions are used to fix values of displacement (

w

) and rotations (

d w / d x

) on the boundary. Such boundary conditions are also called Dirichlet boundary conditions. Load and moment boundary conditions involve higher derivatives of

w

and represent momentum flux. Flux boundary conditions are also called Neumann boundary conditions.

A cantilever beam.

As an example consider a cantilever beam that is built-in at one end and free at the other as shown in the adjacent figure. At the built-in end of the beam there cannot be any displacement or rotation of the beam. This means that at the left end both deflection and slope are zero. Since no external bending moment is applied at the free end of the beam, the bending moment at that location is zero. In addition, if there is no external force applied to the beam, the shear force at the free end is also zero.

Taking the

x

coordinate of the left end as

0

and the right end as

L

(the length of the beam), these statements translate to the following set of boundary conditions (assume

E I

is a constant):

$w|_{x = 0} = 0 \quad ; \quad \frac{\partial w}{\partial x}\bigg|_{x = 0} = 0 \qquad \mbox{(fixed end)}\,$

$\frac{\partial^2 w}{\partial x^2}\bigg|_{x = L} = 0 \quad ; \quad \frac{\partial^3 w}{\partial x^3}\bigg|_{x = L} = 0 \qquad \mbox{(free end)}\,$

A simple support (pin or roller) is equivalent to a point force on the beam which is adjusted in such a way as to fix the position of the beam at that point. A fixed support or clamp, is equivalent to the combination of a point force and a point torque which is adjusted in such a way as to fix both the position and slope of the beam at that point. Point forces and torques, whether from supports or directly applied, will divide a beam into a set of segments, between which the beam equation will yield a continuous solution, given four boundary conditions, two at each end of the segment. Assuming that the product EI is a constant, and defining

λ = F / E I

where F is the magnitude of a point force, and

τ = M / E I

where M is the magnitude of a point torque, the boundary conditions appropriate for some common cases is given in the table below. The change in a particular derivative of w across the boundary as x increases is denoted by

Δ

followed by that derivative. For example,

Δ w'' = w''(x + ) - w''(x - )

where

w''(x + )

is the value of

w''

at the lower boundary of the upper segment, while

w''(x - )

is the value of

w''

at the upper boundary of the lower segment. When the values of the particular derivative are not only continuous across the boundary, but fixed as well, the boundary condition is written e.g.

Δ w'' = 0 *

which actually constitutes two separate equations (e.g.

w''(x - ) = w''(x + )

= fixed).

Boundary	$w'''$	$w''$	$w'$	$w$
Clamp			$Δ w' = 0 *$	$Δ w = 0 *$
Simple support		$Δ w'' = 0$	$Δ w' = 0$	$Δ w = 0 *$
Point force	$Δ w''' = λ$	$Δ w'' = 0$	$Δ w' = 0$	$Δ w = 0$
Point torque	$Δ w''' = 0$	$Δ w'' = τ$	$Δ w' = 0$	$Δ w = 0$
Free end	$w''' = 0$	$w'' = 0$
Clamp at end			$w'$ fixed	$w$ fixed
Simply supported end		$w'' = 0$		$w$ fixed
Point force at end	$w''' = λ$	$w'' = 0$
Point torque at end	$w''' = 0$	$w'' = τ$

Note that in the first cases, in which the point forces and torques are located between two segments, there are four boundary conditions, two for the lower segment, and two for the upper. When forces and torques are applied to an end of the beam, there are two boundary conditions given which apply at that end.

[edit]Loading considerations

Applied loads may be represented either through boundary conditions or through the function

q (x, t)

which represents an external distributed load. Using distributed loading is often favorable for simplicity. Boundary conditions are, however, often used to model loads depending on context; this practice being especially common in vibration analysis.

By nature, the distributed load is very often represented in a piecewise manner, since in practice a load isn't typically a continuous function. Point loads can be modeled with help of the Dirac delta function. For example, consider a static uniform cantilever beam of length

L

with an upward point load

F

applied at the free end. Using boundary conditions, this may be modeled in two ways. In the first approach, the applied point load is approximated by a shear force applied at the free end. In that case the governing equation and boundary conditions are:

$\begin{align} & EI \frac{\mathrm{d}^4 w}{\mathrm{d} x^4} = 0 \\ & w|_{x = 0} = 0 \quad ; \quad \frac{\mathrm{d} w}{\mathrm{d} x}\bigg|_{x = 0} = 0 \quad ; \quad \frac{\mathrm{d}^2 w}{\mathrm{d} x^2}\bigg|_{x = L} = 0 \quad ; \quad -EI \frac{\mathrm{d}^3 w}{\mathrm{d} x^3}\bigg|_{x = L} = F\, \end{align}$

Alternatively we can represent the point load as a distribution using the Dirac function. In that case the equation and boundary conditions are

$\begin{align} & EI \frac{\mathrm{d}^4 w}{\mathrm{d} x^4} = F \delta(x - L) \\ & w|_{x = 0} = 0 \quad ; \quad \frac{\mathrm{d} w}{\mathrm{d} x}\bigg|_{x = 0} = 0 \quad; \quad \frac{\mathrm{d}^2 w}{\mathrm{d} x^2}\bigg|_{x = L} = 0\, \end{align}$

Note that shear force boundary condition (third derivative) is removed, otherwise there would be a contradiction. These are equivalentboundary value problems, and both yield the solution

$w = \frac{F}{6 EI}(3 L x^2 - x^3)\,~.$

The application of several point loads at different locations will lead to

w (x)

being a piecewise function. Use of the Dirac function greatly simplifies such situations; otherwise the beam would have to be divided into sections, each with four boundary conditions solved separately. A well organized family of functions called Singularity functions are often used as a shorthand for the Dirac function, its derivative, and itsantiderivatives.

Dynamic phenomena can also be modeled using the static beam equation by choosing appropriate forms of the load distribution. As an example, the free vibration of a beam can be accounted for by using the load function:

$q(x, t) = \mu \frac{\partial^2 w}{\partial t^2}\,$

where

μ

is the linear mass density of the beam, not necessarily a constant. With this time-dependent loading, the beam equation will be apartial differential equation:

$\frac{\partial^2}{\partial x^2} \left( EI \frac{\partial^2 w}{\partial x^2} \right) = \mu \frac{\partial^2 w}{\partial t^2}.$

Another interesting example describes the deflection of a beam rotating with a constant angular frequency of

ω

$q(x) = \mu \omega^2 w(x)\,$

This is a centripetal force distribution. Note that in this case,

q

is a function of the displacement (the dependent variable), and the beam equation will be an autonomous ordinary differential equation.

[edit]Examples

[edit]Three-point bending

The three point bending test is a classical experiment in mechanics. It represents the case of a beam resting on two roller supports and subjected to a concentrated load applied in the middle of the beam. The shear is constant in absolute value: it is half the central load, P / 2. It changes sign in the middle of the beam. The bending moment varies linearly from one end, where it is 0, and the center where its absolute value is PL / 4, is where the risk of rupture is the most important. The deformation of the beam is described by a polynomial of third degree over a half beam (the other half being symmetrical). The bending moments (

M

) , shear forces (

Q

), and deflections (

w

) for a beam subjected to a central point load and an asymmetric point load are given in the table below.^[6]

Distribution	Max. value
Simply supported beam with central load
$M(x) = \begin{cases} \frac{Px}{2}, & \mbox{for } 0 \le x \le \tfrac{L}{2} \\ \frac{P(L-x)}{2}, & \mbox{for } \tfrac{L}{2} < x \le L \end{cases}$	$M_{L/2} = \tfrac{PL}{4}$
$Q(x) = \begin{cases} \frac{P}{2}, & \mbox{for } 0 \le x \le \tfrac{L}{2} \\ \frac{-P}{2}, & \mbox{for } \tfrac{L}{2} < x \le L \end{cases}$	$\|Q_0\| = \|Q_L\| = \tfrac{P}{2}$
$w(x) = \begin{cases} -\frac{Px(4x^2-3L^2)}{48EI}, & \mbox{for } 0 \le x \le \tfrac{L}{2} \\ \frac{P(x-L)(L^2-8Lx+4x^2)}{48EI}, & \mbox{for } \tfrac{L}{2} < x \le L \end{cases}$	$w_{L/2} = \tfrac{PL^3}{48EI}$
Simply supported beam with asymmetric load
$M(x) = \begin{cases} \tfrac{Pbx}{L}, & \mbox{for } 0 \le x \le a \\ \tfrac{Pbx}{L}-P(x-a)=\tfrac{Pa(L-x)}{L}, & \mbox{for } a < x \le L \end{cases}$	$M_B = \tfrac{Pab}{L}$
$Q(x) = \begin{cases} \tfrac{Pb}{L}, & \mbox{for } 0 \le x \le a \\ -\tfrac{Pb}{L}-P, & \mbox{for } a < x \le L \end{cases}$	$Q_A = \tfrac{Pb}{L}$ $Q_C = \tfrac{Pa}{L}$
$w(x) = \begin{cases} \tfrac{Pbx(L^2-b^2-x^2)}{6LEI}, & 0 \le x \le a \\ \tfrac{Pbx(L^2-b^2-x^2)}{6LEI}+\tfrac{P(x-a)^3}{6EI}, & a < x \le L \end{cases}$	$w_{\mathrm{max}} = \tfrac{\sqrt{3}Pb(L^2-b^2)^{\frac{3}{2}}}{27LEI}$ at $x = \sqrt{\tfrac{L^2-b^2}{3}}$

[edit]Cantilever beams

Another important class of problems involves cantilever beams. The bending moments (

M

) , shear forces (

Q

), and deflections (

w

) for a cantilever beam subjected to a point load at the free end and a uniformly distributed load are given in the table below.^[6]

Distribution	Max. value
Cantilever beam with end load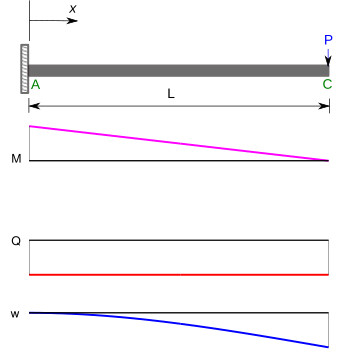
$M (x) = P (x - L)$	$M A = P L$
$Q (x) = P$	$Q max = P$
$w(x) = \tfrac{Px^2(3L-x)}{6EI}$	$w_C = \tfrac{PL^3}{3EI}$
Cantilever beam with uniformly distributed load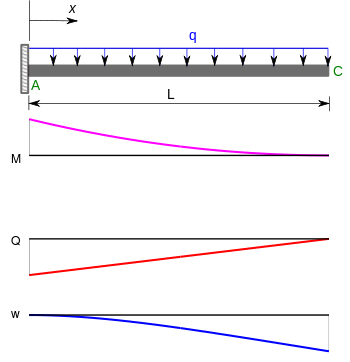
$M(x) =-\tfrac{q(L^2-2Lx+x^2)}{2}$	$M_A = \tfrac{qL^2}{2}$
$Q (x) = q (L - x),$	$Q A = q L$
$w(x) = \tfrac{qx^2(6L^2-4Lx+x^2)}{24EI}$	$w_C = \tfrac{qL^4}{8EI}$

Solutions for several other commonly encountered configurations are readily available in textbooks on mechanics of materials and engineering handbooks.

[edit]Statically indeterminate beams

The bending moments and shear forces in Euler-Bernoulli beams can often be determined directly using static balance of forces andmoments. However, for certain boundary conditions, the number of reactions can exceed the number of independent equilibrium equations.^[6]Such beams are called statically indeterminate.

The built-in beams shown in the figure below are statically indeterminate. To determine the stresses and deflections of such beams, the most direct method is to solve the Euler–Bernoulli beam equation with appropriate boundary conditions. But direct analytical solutions of the beam equation are possible only for the simplest cases. Therefore, additional techniques such as linear superposition are often used to solve statically indeterminate beam problems.

The superposition method involves adding the solutions of a number of statically determinate problems which are chosen such that the boundary conditions for the sum of the individual problems add up to those of the original problem.

(a) Uniformly distributed load q.	(b) Linearly distributed load with maximum q₀
$M_{\mathrm{max}} = \cfrac{qL^2}{12} ~;~~ w_{\mathrm{max}} = \cfrac{qL^4}{384EI}$
(c) Concentrated load P	(d) Moment M₀

Another commonly encountered statically indeterminate beam problem is the cantilevered beam with the free end supported on a roller.^[6] The bending moments, shear forces, and deflections of such a beam are listed below.

Distribution	Max. value
$M(x) = -\tfrac{q}{8}(L^2-5Lx+4x^2)$	$\begin{align} M_B & = -\tfrac{9qL^2}{128} \mbox{ at } x=\tfrac{5L}{8}\\ M_A & = \tfrac{qL^2}{8} \end{align}$
$Q(x) = -\tfrac{q}{8}(8x -5L)$	$Q_A = -\tfrac{5qL}{8}$
$w(x) = \tfrac{qx^2}{48EI}(3L^2-5Lx+2x^2)$	$w_{\mathrm{max}} = \tfrac{qL^4}{185EI} \mbox{ at } x=0.5785L$

[edit]Extensions

The kinematic assumptions upon which the Euler-Bernoulli beam theory is founded allow it to be extended to more advanced analysis. Simple superposition allows for three-dimensional transverse loading. Using alternative constitutive equations can allow for viscoelastic orplastic beam deformation. Euler-Bernoulli beam theory can also be extended to the analysis of curved beams, beam buckling, composite beams, and geometrically nonlinear beam deflection.

Euler-Bernoulli beam theory does not account for the effects of transverse shear strain. As a result it underpredicts deflections and overpredicts natural frequencies. For thin beams (beam length to thickness ratios of the order 20 or more) these effects are of minor importance. For thick beams, however, these effects can be significant. More advanced beam theories such as the Timoshenko beam theory(developed by the Russian-born scientist Stephen Timoshenko) have been developed to account for these effects.

[edit]Large deflections

Euler-Bernoulli beam

The original Euler-Bernoulli theory is valid only for infinitesimal strains and small rotations. The theory can be extended in a straightforward manner to problems involving moderately large rotations provided that the strain remains small by using the von Kármán strains.^[7]

The Euler-Bernoulli hypotheses that plane sections remain plane and normal to the axis of the beam lead to displacements of the form

$v_1 = v_0(x) - z \cfrac{dw_0}{dx} ~;~~v_2 = 0 ~;~~ v_3 = w_0(x)$

Using the definition of the Lagrangian Green strain from finite strain theory, we can find the von Karman strains for the beam that are valid for large rotations but small strains. These strains have the form

$\begin{align} \varepsilon_{11} & = \cfrac{du_0}{dx_1} - x_3\cfrac{d^2w_0}{dx_1^2} + \frac{1}{2}\left[ \left(\cfrac{du_0}{dx_1}-x_3\cfrac{d^2w_0}{dx_1^2}\right)^2 + \left(\cfrac{dw_0}{dx_1}\right)^2\right] \\ \varepsilon_{22} & = 0 \\ \varepsilon_{33} & = \frac{1}{2}\left(\cfrac{dw_0}{dx_1}\right)^2 \\ \varepsilon_{23} & = 0 \\ \varepsilon_{31} & = \frac{1}{2}\left(\cfrac{dw_0}{dx_1}-\cfrac{dw_0}{dx_1}\right) - \frac{1}{2}\left[\left(\cfrac{du_0}{dx_1}-x_3\cfrac{d^2w_0}{dx_1^2}\right) \left(\cfrac{dw_0}{dx_1}\right)\right] \\ \varepsilon_{12} & = 0 \end{align}$

From the principle of virtual work, the balance of forces and moments in the beams gives us the equilibrium equations

$\begin{align} \cfrac{dN_{xx}}{dx} + f(x) & = 0 \\ \cfrac{d^2M_{xx}}{dx^2} + q(x) + \cfrac{d}{dx}\left(N_{xx}\cfrac{dw_0}{dx}\right) & = 0 \end{align}$

where

f (x)

is the axial load,

q (x)

is the transverse load, and

$N_{xx} = \int_A \sigma_{xx}~ dA ~;~~ M_{xx} = \int_A z\sigma_{xx}~ dA$

To close the system of equations we need the constitutive equations that relate stresses to strains (and hence stresses to displacements). For large rotations and small strains these relations are

$\begin{align} N_{xx} & = A_{xx}\left[\cfrac{du_0}{dx} + \frac{1}{2}\left(\cfrac{dw_0}{dx}\right)^2 \right] - B_{xx}\cfrac{d^2w_0}{dx^2} \\ M_{xx} & = B_{xx}\left[\cfrac{du_0}{dx} + \frac{1}{2}\left(\cfrac{dw_0}{dx}\right)^2 \right] - D_{xx}\cfrac{d^2w_0}{dx^2} \end{align}$

where

$A_{xx} = \int_A E~dA ~;~~ B_{xx} = \int_A zE~dA ~;~~ D_{xx} = \int_A z^2E~dA ~.$

The quantity

A x x

is the extensional stiffness,

B x x

is the coupled extensional-bending stiffness, and

D x x

is the bending stiffness.

For the situation where the beam has a uniform cross-section and no axial load, the governing equation for a large-rotation Euler-Bernoulli beam is

$EI~\cfrac{\mathrm{d}^4 w}{\mathrm{d}x^4} - \frac{3}{2}~EA~\left(\cfrac{\mathrm{d} w}{\mathrm{d}x}\right)^2\left(\cfrac{\mathrm{d}^2 w}{\mathrm{d}x^2}\right) = q(x)$

[edit]See also

Applied mechanics
Bending
Buckling
Flexural rigidity
Plate theory
Sandwich theory
Singularity function
Strain (materials science)
Theorem of three moments (Clapeyron's theorem)
Three point flexural test

[edit]Notes

^ Timoshenko, S., (1953), History of strength of materials, McGraw-Hill New York
^ Truesdell, C., (1960), The rational mechanics of flexible or elastic bodies 1638-1788, Venditioni Exponunt Orell Fussli Turici.
^ Ballarini, Roberto (April 18, 2003). "The Da Vinci-Euler-Bernoulli Beam Theory?". Mechanical Engineering Magazine Online. Retrieved 2006-07-22.
^ Seon M. Han, Haym Benaroya and Timothy Wei (March 22, 1999) (PDF). Dynamics of Transversely Vibrating Beams using four Engineering Theories. final version. Academic Press. Retrieved 2007-04-15.
^ McKenzie, William (2006). Examples in Structural Analysis. Taylor & Francis.
^ ^a ^b ^c ^d ^e ^f ^g ^h Gere, J. M. and Timoshenko, S. P., 1997, Mechanics of Materials, PWS Publishing Company.
^ Reddy, J. N., (2007), Nonlinear finite element analysis, Oxford University Press.

[edit]References

E.A. Witmer (1991-1992). "Elementary Bernoulli-Euler Beam Theory". MIT Unified Engineering Course Notes. pp. 5–114 to 5–164.

Euler-Bernoulli balok teori

Dari Wikipedia, ensiklopedia bebas

Artikel ini membutuhkan tambahan citations untuk verifikasi . Harap membantu memperbaiki artikel ini dengan menambahkan citations ke sumber terpercaya . Unsourced bahan mungkincacat dan dihapus . (November 2008)

Continuum mekanika

Hukum[show]
Padat mekanika [hide] Padat Stres · Deformasi Kesesuaian Finite strain · ketegangan Terkecil Elastisitas ( linier ) · Plastisitas Bending · Hooke hukum Kegagalan teori Mekanika perpatahan Gesekan / Friksional Kontak mekanika
Mekanika fluida [show]
Rheology [show]
Para ilmuwan[show]
v d e

Ini balok kaca bergetar dapat dimodelkan sebagai balok kantilever dengan akselerasi, densitas linier variabel, modulus penampang variabel, beberapa jenis disipasi, pemuatan akhir kenyal, dan mungkin suatu massa titik di ujung bebas.

Euler-Bernoulli teori balok (juga dikenal sebagai teori balok insinyur atau teori balok klasik) ^[1] adalah penyederhanaan linier teori elastisitas yang menyediakan sarana untuk menghitung beban-membawa dan defleksi karakteristik balok . Ini mencakup kasus untuk defleksi kecil dari balok yang mengalami beban lateral saja. Dengan demikian kasus khusus dari teori balok Timoshenko yang menyumbang deformasi geser dan berlaku untuk balok tebal.Pertama kali diucapkan sekitar tahun 1750, ^[2] tetapi tidak diterapkan dalam skala besar sampai pengembangan dari Menara Eiffel dan kincir raksasa di akhir abad 19. Mengikuti demonstrasi yang sukses, dengan cepat menjadi landasan teknik dan enabler dari Revolusi Industri Kedua .

Alat analisis tambahan telah dikembangkan seperti teori piring dan analisis elemen hingga , tetapi kesederhanaan teori balok membuatnya menjadi alat penting dalam ilmu, terutamastruktural dan teknik mesin .

[ sunting ]Sejarah

Skema penampang dari balok bengkok menampilkan sumbu netral.

Konsensus yang berlaku adalah bahwa Galileo Galilei membuat upaya pertama untuk mengembangkan teori balok, tetapi studi terbaru menyatakan bahwa Leonardo da Vinci adalah yang pertama untuk membuat pengamatan penting. Da Vinci tidak memiliki hukum Hooke dan kalkulus untuk menyelesaikan teori, sedangkan Galileo ditahan oleh asumsi yang salah yang dibuatnya. ^[3]

Sinar Bernoulli ini dinamai Jacob Bernoulli , yang membuat penemuan penting. Leonhard Euler dan Daniel Bernoulli adalah yang pertama untuk menyusun teori yang berguna sekitar tahun 1750. ^[4] Pada saat, ilmu pengetahuan dan rekayasa pada umumnya dilihat sebagai bidang yang sangat berbeda, dan ada keraguan yang cukup bahwa produk matematika dari akademisi dapat dipercaya untuk aplikasi keamanan praktis. Jembatan dan bangunan terus dirancang oleh preseden sampai akhir abad 19, ketikaMenara Eiffel dan kincir raksasa menunjukkan validitas teori dalam skala besar.

Untuk tujuan praktis, seperti dalam kode desain Eropa, sekarang telah digantikan oleh susu formula Robertson Perry yang mempertimbangkan defleksi awal balok. ^[5]

[ sunting ]persamaan statis balok

Bending dari sinar Euler-Bernoulli. Setiap penampang balok berada pada 90 derajat terhadap sumbu netral.

Persamaan Euler-Bernoulli menggambarkan hubungan antara balok itudefleksi dan beban yang diterapkan ^[6] :

$\ Frac {\ mathrm {} d ^ 2} {\ mathrm {} d x ^ 2} \ left (EI \ frac {\ mathrm {} d ^ 2 w} {\ mathrm {} d x ^ 2} \ right) = q. \,$

$W$ kurva $(x)$ menggambarkan $w$ defleksi balok pada beberapa posisi $x$ (ingat bahwa balok dimodelkan sebagai objek satu dimensi). $Q$ adalah beban terdistribusi, dengan kata lain gaya per satuan panjang (analog dengantekanan menjadi gaya per area), itu mungkin merupakan fungsi dari $x, w,$ atau variabel lain.

Perhatikan bahwa $E$ adalah modulus elastisitas dan bahwa $saya$ adalahmomen kedua daerah . $Saya$ harus dihitung sehubungan dengan tegak lurus sumbu pusat massa pada beban yang diterapkan. Untuk Euler-Bernoulli balok tidak dalam beban aksial sumbu ini disebut sumbu netral .

Seringkali,

w = w (x), q = q (x),

dan EI adalah konstan, sehingga:

$EI \ frac {\ mathrm {} d ^ 4 w} {\ mathrm {} d x ^ 4} = q (x). \,$

Persamaan ini, menggambarkan defleksi balok, seragam statis, digunakan secara luas dalam praktek rekayasa. Ekspresi ditabulasi untuk $w$ defleksi balok untuk konfigurasi umum dapat ditemukan dalam buku-buku pedoman teknik. Untuk situasi yang lebih rumit defleksi dapat ditentukan dengan memecahkan persamaan Euler-Bernoulli dengan menggunakan teknik seperti " metode lendutan kemiringan "," saat metode distribusi "," metode saat daerah , " konjugat balok metode "," prinsip kerja virtual "," integrasi langsung "," metode Castigliano itu ","metode Macaulay "atau" metode kekakuan langsung ".

Derivatif berturut $w$ memiliki arti penting:

$\ Textstyle {w} \,$ adalah defleksi.
$\ Textstyle {\ frac {\ mathrm {d} w} {\ mathrm {d} x}} = \ varphi \,$ adalah kemiringan balok.
$- \ Textstyle {EI \ frac {\ mathrm {d} ^ 2 w} {\ mathrm {d} x ^ 2}} = M \,$ adalah momen lentur pada balok.
$\ Textstyle {- \ frac {\ mathrm {d}} {\ mathrm {d} x} \ left (EI \ frac {\ mathrm {d} ^ 2 w} {\ mathrm {d} x ^ 2} \ right) = Q} \,$ adalah gaya geser pada balok.

Tegangan pada balok dapat dihitung dari ekspresi di atas setelah lendutan akibat beban yang diberikan telah ditentukan.

Sejumlah konvensi tanda yang berbeda dapat ditemukan dalam literatur pada lentur dari balok dan perawatan harus dilakukan untuk menjaga konsistensi. ^[6] Pada artikel ini, konvensi tanda telah dipilih sehingga sistem koordinat tangan kanan . Gaya yang bekerja dalam arah $x$ positif dan $z$ diasumsikan positif. Tanda momen lentur dipilih sehingga nilai positif mengarah pada tegangan tarik pada kabel bawah. Tanda dari gaya geser telah dipilih sedemikian rupa sehingga sesuai dengan tanda momen lentur.

[ sunting ]Dinamis persamaan balok

Elemen hingga metode model getaran sinar lebar flange ( I-balok ).

Persamaan balok dinamis adalah persamaan Euler-Lagrange untuk tindakan berikut

$S = \ int_0 ^ L \ left [\ frac {1} {2} \ mu \ left (\ frac {\ partial w} {\ partial t} \ right) ^ 2 - \ frac {1} {2} EI \ kiri (\ frac {\ partial ^ 2 w} {\ partial x ^ 2} \ right) ^ 2 + q (x) w (x t) \ right] dx$

Istilah pertama merupakan energi kinetik mana

μ

adalah massa per satuan panjang; yang kedua merupakan energi potensial karena kekuatan internal (bila dianggap dengan tanda negatif) dan istilah ketiga merupakan energi potensial akibat beban $q$ eksternal

(x).

Para persamaan Euler-Lagrangedigunakan untuk menentukan fungsi yang meminimalkan $S$ fungsional. Untuk Euler-Bernoulli dinamis balok, persamaan Euler-Lagrange adalah

$\ Cfrac {\ partial ^ 2} {\ partial x ^ 2} \ left (EI \ cfrac {\ partial ^ 2 w} {\ partial x ^ 2} \ right) = - \ mu \ cfrac {\ partial ^ 2 w } {\ partial t ^ 2} + q (x)$

[show]Penurunan Euler-Lagrange persamaan untuk balok

[ sunting ]Stres

Selain lendutan, persamaan balok menggambarkan kekuatan dan saat-saat dan dengan demikian dapat digunakan untuk menggambarkanstres . Untuk alasan ini, Euler-Bernoulli balok persamaan banyak digunakan dalam rekayasa , terutama sipil dan mesin, untuk menentukan kekuatan (serta lendutan) balok bawah membungkuk.

Baik saat lentur dan gaya geser menyebabkan menekankan pada balok. Tegangan akibat gaya geser maksimum di sepanjang sumbu netraldari balok (bila lebar balok, t, adalah konstan sepanjang penampang balok, jika tidak integral yang melibatkan saat pertama dan lebar balok yang perlu dievaluasi untuk penampang tertentu), dan tegangan tarik maksimum adalah baik di permukaan atas atau bawah. Jadi maksimumtegangan utama dalam berkas mungkin tidak di permukaan maupun di pusat tetapi di beberapa area umum. Namun, tekanan gaya geser dapat diabaikan dibandingkan dengan tekanan momen lentur dalam semua tetapi stockiest balok serta fakta bahwa konsentrasi teganganyang umum terjadi pada permukaan, yang berarti bahwa tegangan maksimum pada balok mungkin akan di permukaan.

[ sunting ]Sederhana atau simetris lentur

Elemen dari sinar bengkok: serat membentuk busur konsentris, serat atas dikompresi dan serat bawah melar.

Untuk balok lintas-bagian yang simetris terhadap bidang tegak lurus terhadap bidang netral, dapat ditunjukkan bahwa tegangan tarik yang dialami balok dapat dinyatakan sebagai:

$\ Sigma = \ frac {Mz} {I} =-ze ~ \ frac {\ mathrm {d} ^ 2 w} {\ mathrm {d} x ^ 2} \,.$

Di sini, $z$ adalah jarak dari sumbu netral ke tempat tujuan; dan $M$ adalah momen lentur. Perhatikan bahwa persamaan ini menyiratkan bahwa lentur murni (tanda positif) akan menyebabkan stres nol pada sumbu netral, positif (tarik) stres di "atas" dari balok, dan negatif (tekan) stres di bagian bawah balok, dan juga menyiratkan bahwa tegangan maksimum akan berada pada permukaan atas dan minimum di bagian bawah. Ini tegangan lentur dapat ditumpangkan dengan tegangan aksial diterapkan, yang akan menimbulkan pergeseran sumbu (nol stres) netral.

[ sunting ]Maksimum tegangan pada penampang

Besaran yang digunakan dalam definisi modulus bagian balok.

Tegangan tarik maksimum pada bagian lintas berada pada lokasi

z = c 1

dan tegangan tekan maksimum adalah di lokasi

z = - c 2

dimana ketinggian penampang adalah

h = c 1 + c 2.

Ini adalah tekanan

$\ Sigma_1 = \ {cfrac Mc_1} {I} = \ cfrac {M} {} ~ S_1; ~ ~ \ sigma_2 = - \ cfrac {Mc_2} {I} = - \ cfrac {M} {} S_2$

Kuantitas

S 1, S 2

adalah bagian modulus ^[6] dan didefinisikan sebagai

$S_1 = \ cfrac {I} {} ~ c_1; ~ ~ S_2 = \ cfrac {I} {} c_2$

Modulus bagian menggabungkan semua informasi geometris penting tentang bagian sinar ke dalam satu kuantitas. Untuk kasus di mana balok adalah ganda simetris,

c 1 = c 2

dan kita memiliki satu bagian modulus

S = I / c.

[ sunting ]Saring dalam Euler-Bernoulli balok

Kami membutuhkan ekspresi untuk ketegangan dalam hal defleksi permukaan netral untuk berhubungan tekanan dalam sebuah berkas Euler-Bernoulli untuk defleksi. Untuk mendapatkan ekspresi yang kita gunakan asumsi bahwa normals ke permukaan netral tetap normal selama deformasi dan bahwa defleksi kecil. Asumsi ini berarti bahwa lengkungan balok ke dalam busur lingkaran radius

ρ

(lihat Gambar 1) dan bahwa permukaan netral tidak berubah panjangnya selama deformasi. ^[6]

Mari

d x

adalah panjang elemen dari permukaan netral di negara bagian pelat badan kaku. Untuk defleksi kecil, elemen tidak berubah panjangnya usai menekuk tetapi deformasi ke busur lingkaran radius

ρ.

Jika

dθ

adalah sudut subtended oleh busur ini, maka $\ Mathrm {d} x = \ rho ~ \ mathrm {d} \ theta$ .

Mari kita mempertimbangkan segmen lain dari elemen pada jarak $z$ di atas permukaan netral. Panjang awal elemen ini adalah

d x.

Namun, setelah membungkuk, panjang elemen ini menjadi $\ Mathrm {d} x '= (\ rho-z) ~ \ mathrm {d} \ theta = \ mathrm {d} x - z ~ \ mathrm {d} \ theta$ . Ketegangan di segmen balok diberikan oleh

$\ Varepsilon_x = \ cfrac {\ mathrm {d} x'-\ mathrm {d} x} {\ mathrm {d} x} = - \ cfrac {z} {\ rho} = - \ kappa ~ z$

mana

κ

adalah kelengkungan balok. Ini memberikan kita regangan aksial dalam berkas sebagai fungsi jarak dari permukaan netral. Namun, kita masih perlu mencari hubungan antara jari-jari kelengkungan dan $w$ defleksi balok.

[ sunting ]Hubungan antara kelengkungan dan balok defleksi

Misalkan P menjadi titik pada permukaan netral balok pada $x$ jarak dari asal-usul $(x, z)$ sistem koordinat. Kemiringan balok, yaitu sudut yang dibuat oleh permukaan netral dengan sumbu $x,$ pada titik ini adalah

$\ Theta (x) = \ cfrac {\ mathrm {d} w} {\ mathrm {d} x}$

Oleh karena itu, untuk sebuah elemen yang sangat kecil

d x,

relasi $\ Mathrm {d} x = \ rho ~ \ mathrm {d} \ theta$ dapat ditulis sebagai

$\ Cfrac {1} {\ rho} = \ cfrac {\ mathrm {d} \ theta} {\ mathrm {d} x} = \ cfrac {\ mathrm {d} ^ 2w} {\ mathrm {d} x ^ 2 } = \ kappa$

Maka regangan pada balok dapat dinyatakan sebagai

$\ Varepsilon_ {x} =-z \ cfrac {\ mathrm {d} ^ 2w} {\ mathrm {d} x ^ 2}$

[ sunting ]Stres-regangan hubungan

Untuk satu dimensi linier elastis bahan, stres tersebut terkait dengan ketegangan dengan $\ Sigma = E \ varepsilon$ di mana $E$ adalah modulus Young .Karena itu stres dalam Euler-Bernoulli balok diberikan oleh

$\ Sigma_x =-ze \ cfrac {\ mathrm {d} ^ 2w} {\ mathrm {d} x ^ 2}$

Perhatikan bahwa hubungan diatas, jika dibandingkan dengan hubungan antara tegangan aksial dan momen lentur, menyebabkan

$M =-EI \ cfrac {\ mathrm {d} ^ 2w} {\ mathrm {d} x ^ 2}$

Karena gaya geser diberikan oleh

Q = d M / d x,

kami juga memiliki

$Q =-EI \ cfrac {\ mathrm {d} ^ 3u} {\ mathrm {d} x ^ 3}$

[ sunting ]Batas pertimbangan

Persamaan balok mengandung turunan orde-keempat dalam $x.$ Untuk menemukan solusi unik $w (x, t),$ kita perlu empat kondisi batas.Kondisi batas biasanya model yang mendukung, tetapi mereka juga dapat model beban terpusat, beban didistribusikan dan momen. Kondisidukungan atau perpindahan batas digunakan untuk memperbaiki nilai-nilai perpindahan $(w)$ dan rotasi

(d b / d x)

pada batas. Kondisi batas tersebut juga disebut kondisi batas Dirichlet . Beban dan kondisi batas saat melibatkan turunan yang lebih tinggi dari $w$ dan mewakili fluks momentum . Kondisi batas fluks juga disebut kondisi batas Neumann .

Sebuah balok kantilever.

Sebagai contoh mempertimbangkan kantilever balok yang built-in di satu ujung dan gratis di lain seperti yang ditunjukkan pada gambar yang berdekatan. Pada akhir built-in balok tidak bisa ada setiap perpindahan atau rotasi balok. Ini berarti bahwa di ujung kiri baik lendutan dan kemiringan adalah nol. Karena tidak ada momen lentur eksternal diterapkan pada ujung bebas dari balok, momen lentur di lokasi itu adalah nol. Selain itu, jika tidak ada gaya eksternal diterapkan pada balok, gaya geser pada ujung bebas juga nol.

Mengambil koordinat $x$ dari ujung kiri sebagai

0

dan ujung kanan sebagai $L$ (panjang balok), laporan menerjemahkan ke set berikut kondisi batas (menganggap $saya E$ adalah konstanta):

$w | _ {x = 0} = 0 \ quad; \ quad \ frac {\ partial w} {\ partial x} \ Bigg | _ {x = 0} = 0 \ qquad \ mbox {(akhir tetap)} \,$

$\ Frac {\ partial ^ 2 w} {\ partial x ^ 2} \ Bigg | _ {x = L} = 0 \ quad; \ quad \ frac {\ partial w ^ 3} {\ partial x ^ 3} \ Bigg | _ {x = L} = 0 \ qquad \ mbox {(akhir gratis)} \,$

Sebuah dukungan sederhana (pin atau rol) adalah setara dengan kekuatan titik pada balok yang disesuaikan sedemikian rupa sehingga memperbaiki posisi balok pada saat itu. Sebuah dukungan tetap atau penjepit, setara dengan kombinasi kekuatan dan torsi titik titik yang disesuaikan sedemikian rupa untuk memperbaiki kedua posisi dan kemiringan balok pada saat itu. Titik kekuatan dan torsi, baik dari dukungan atau langsung diterapkan, akan membagi balok menjadi satu set segmen, antara yang persamaan balok akan menghasilkan solusi berkesinambungan, mengingat empat kondisi batas, dua di setiap akhir segmen. Dengan asumsi bahwa produk EI adalah konstanta, dan mendefinisikan

λ = F / E I

dimana F adalah besarnya kekuatan titik, dan

τ = M / E saya

di mana M adalah besarnya torsi titik, kondisi batas yang sesuai untuk beberapa kasus umum diberikan dalam tabel dibawah ini. Perubahan turunan tertentu w melintasi batas sebagai xmeningkat dilambangkan dengan

Δ

diikuti oleh derivatif yang. Sebagai contoh,

Δ w = w'''' (x +) - w'' (x -)

dimana

w'' (x +)

adalah nilai

w''

pada batas bawah dari segmen atas, sedangkan

w''(x -)

adalah nilai

dari'' w

pada batas atas dari segmen bawah. Ketika nilai-nilai dari derivatif tertentu tidak hanya terus menerus di batas, tetapi tetap juga, syarat batas ditulis misalnya

Δ w'' = 0 *

yang sebenarnya merupakan dua persamaan yang terpisah (misalnya

w'' (x -) = w'' (x +)

= tetap).

Batas	$w'''$	$w''$	$w'$	$w$
Klem			$Δ w'= 0 *$	$Δ w = 0 *$
Sederhana dukungan		$Δ w'' = 0$	$Δ w'= 0$	$Δ w = 0 *$
Titik kekuatan	$Δ w'''= λ$	$Δ w'' = 0$	$Δ w'= 0$	$Δ w = 0$
Titik torsi	$Δ w'''= 0$	$Δ w'' = τ$	$Δ w'= 0$	$Δ w = 0$
Gratis akhir	$w'''= 0$	$'' w = 0$
Clamp pada akhir			$w$ tetap $'$	$w$ tetap
Cukup didukung akhir		$'' w = 0$		$w$ tetap
Titik berlaku pada akhir	$w'''= λ$	$'' w = 0$
Titik torsi pada akhir	$w'''= 0$	$w'' = τ$

Perhatikan bahwa dalam kasus pertama, di mana pasukan titik dan torsi terletak antara dua segmen, ada kondisi batas empat, dua untuk segmen bawah, dan dua untuk bagian atas. Ketika pasukan dan torsi yang diterapkan pada akhir balok, ada dua kondisi batas yang diberikan yang berlaku pada akhir itu.

[ sunting ]Loading pertimbangan

Beban Terapan dapat diwakili baik melalui kondisi batas atau melalui fungsi

q (x, t)

yang merupakan mendistribusikan beban eksternal.Menggunakan pemuatan didistribusikan sering menguntungkan untuk kesederhanaan. Kondisi batas yang, bagaimanapun, sering digunakan untuk beban Model tergantung pada konteks; praktik ini menjadi sangat umum dalam analisis getaran.

Secara alami, beban didistribusikan sangat sering diwakili dengan cara sesepenggal, karena dalam praktek beban tidak biasanya sebuah fungsi kontinu. Beban terpusat dapat dimodelkan dengan bantuan dari fungsi delta Dirac . Sebagai contoh, pertimbangkan sebuah balok kantilever statis seragam panjang

L

dengan beban titik

F

ke atas diterapkan pada ujung bebas. Menggunakan kondisi batas, hal ini dapat dimodelkan dengan dua cara. Dalam pendekatan pertama, beban titik diterapkan diperkirakan dengan gaya geser diterapkan pada ujung bebas. Dalam hal ini persamaan dan kondisi batas yang mengatur adalah:

$\ Begin {align} & EI \ frac {\ mathrm {d} ^ 4 w} {\ mathrm {d} x ^ 4} = 0 \ \ & w | _ {x = 0} = 0 \ quad; \ quad \ frac {\ mathrm {d} w} {\ mathrm {d} x} \ Bigg | _ {x = 0} = 0 \ quad; \ quad \ frac {\ mathrm {d} ^ 2 w} {\ mathrm {d } x ^ 2} \ Bigg | _ {x = L} = 0 \ quad; \ quad-EI \ frac {\ mathrm {d} ^ 3 w} {\ mathrm {d} x ^ 3} \ Bigg | _ { x = L} = F \, \ end {align}$

Atau kita dapat mewakili beban titik sebagai distribusi menggunakan fungsi Dirac. Dalam hal ini kondisi persamaan dan batas adalah

$\ Begin {align} & EI \ frac {\ mathrm {} d ^ 4 w} {\ mathrm {} d x ^ 4} = M \ delta (x - L) \ \ & w | _ {x = 0} = 0 \ quad; \ quad \ frac {\ mathrm {d} w} {\ mathrm {d} x} \ Bigg | _ {x = 0} = 0 \ quad; \ quad \ frac {\ mathrm {d} ^ 2 w} {\ mathrm {d} x ^ 2} \ Bigg | _ {x = L} = 0 \, \ end {align}$

Perhatikan bahwa kekuatan syarat batas geser (turunan ketiga) akan dihapus, jika tidak akan ada kontradiksi. Ini adalah setara masalah nilai batas , dan keduanya menghasilkan solusi

$w = \ frac {F} {6} EI (3 L x ^ 2 - x ^ 3) \, ~.$

Penerapan beban terpusat beberapa lokasi yang berbeda akan menyebabkan $w (x)$ menjadi fungsi sesepenggal. Penggunaan fungsi Dirac sangat menyederhanakan situasi seperti itu, jika tidak balok harus dibagi menjadi beberapa bagian, masing-masing dengan empat kondisi batas diselesaikan secara terpisah. Sebuah keluarga yang terorganisir dari fungsi disebut fungsi Singularity sering digunakan sebagai singkatan untuk fungsi Dirac, yang turunan , dan yang antiderivatives .

Fenomena dinamis juga dapat dimodelkan dengan menggunakan persamaan balok statis dengan memilih formulir yang sesuai dari distribusi beban. Sebagai contoh, bebas getaran dari balok dapat dipertanggungjawabkan dengan menggunakan fungsi beban:

$q (x, t) = \ mu \ frac {\ partial ^ 2 w} {\ partial t ^ 2} \,$

di mana

μ

adalah kepadatan massa linear balok, tidak selalu konstan. Dengan pemuatan bergantung waktu, persamaan balok akan menjadipersamaan diferensial parsial :

$\ Frac {\ partial ^ 2} {\ partial x ^ 2} \ left (EI \ frac {\ partial ^ 2 w} {\ partial x ^ 2} \ right) = \ mu \ frac {\ partial ^ 2 w} {\ partial t ^ 2}.$

Contoh lain yang menarik menggambarkan defleksi sinar berputar dengan konstan frekuensi sudut

ω

dari:

$q (x) = \ mu \ omega ^ 2 w (x) \,$

Ini adalah gaya sentripetal distribusi. Perhatikan bahwa dalam kasus ini, $q$ adalah fungsi dari perpindahan (variabel dependen), dan persamaan balok akan menjadi otonom persamaan diferensial biasa .

[ sunting ]Contoh

[ sunting ]Tiga titik lentur

Tiga titik uji lentur adalah eksperimen klasik dalam mekanika. Ini merupakan kasus balok bertumpu pada dua mendukung roller dan dikenakan beban terpusat diterapkan di tengah balok. Geser adalah konstan dalam nilai absolut: ia adalah setengah beban pusat, P / 2. Ia mengubah tanda di tengah balok. Momen lentur bervariasi secara linear dari satu ujung, di mana itu adalah 0, dan pusat di mana nilai absolut adalah PL / 4, adalah di mana resiko pecah adalah yang paling penting. Deformasi balok digambarkan oleh polinomial derajat ketiga atas balok setengah (setengah lainnya yang simetris). Momen lentur $(M),$ gaya geser $(Q),$ dan defleksi $(w)$ untuk balok dikenai beban titik pusat dan titik beban asimetris diberikan dalam tabel di bawah ini. ^[6]

Distribusi	Max. nilai
Cukup didukung balok dengan beban pusat
$M (x) = \ begin {kasus} \ frac {Px} {2}, & \ mbox {untuk} 0 \ le x \ le \ tfrac {L} {2} \ \ \ frac {P (Lx)} { 2}, & \ mbox {untuk} \ {L} tfrac {2} <L x \ le \ end {} kasus$	$M_ {L / 2} = \ {tfrac PL} {4}$
$Q (x) = \ begin {kasus} \ frac {P} {2}, & \ mbox {untuk} 0 \ le x \ le \ tfrac {L} {2} \ \ \ frac {-P} {2} , & \ mbox {untuk} \ tfrac {L} {2} <x \ le L \ end {} kasus$	$\| Q_0 \| = \| Q_L \| = \ tfrac {P} {2}$
$w (x) = \ begin {kasus} - \ frac {Px (4x ^ 2-3L ^ 2)} {} 48EI, & \ mbox {untuk} 0 \ le x \ le \ tfrac {L} {2} \ \ \ frac {P (xL) (L ^ 2-8Lx +4 x ^ 2)} {} 48EI, & \ mbox {untuk} \ tfrac {L} {2} <x \ le L \ end {} kasus$	$W_ {L / 2} = \ {tfrac PL ^ 3} {} 48EI$
Cukup didukung balok dengan beban asimetris
$M (x) = \ begin {kasus} \ {tfrac PBX} {L}, & \ mbox {untuk} 0 \ le x \ le a \ \ \ tfrac {PBX} {L}-P (xa) = \ tfrac {Pa (Lx)} {L}, & \ mbox {untuk} a <x \ le L \ end {} kasus$	$M_B = \ {tfrac PAB} {L}$
$Q (x) = \ begin {kasus} \ {tfrac Pb} {L}, & \ mbox {untuk} 0 \ le x \ le a \ \ - \ tfrac {Pb} {L}-P, & \ mbox { untuk} a <x \ le L \ end {} kasus$	$Q_A = \ {tfrac Pb} {L}$ $Q_C = \ {tfrac Pa} {L}$
$w (x) = \ begin {kasus} \ {tfrac PBX (L ^ 2-b ^ 2-x ^ 2)} {} 6LEI, & 0 \ le x \ le a \ \ \ tfrac {PBX (L ^ 2 -b ^ 2-x ^ 2)} {6LEI} + \ tfrac {P (xa) ^ 3} {6EI}, & sebuah <x \ L le \ end {} kasus$	$W_ {\ mathrm {max}} = \ tfrac {\ sqrt {3} Pb (L ^ 2-b ^ 2) ^ {\ frac {3} {2}}}} {27LEI$ di $x = \ sqrt {\ tfrac {L ^ 2-b ^ 2} {3}}$

[ sunting ]balok kantilever

Kelas lain penting dari masalah melibatkan kantilever balok. Momen lentur $(M),$ gaya geser $(Q),$ dan defleksi $(w)$ untuk balok kantilever dikenakan beban titik di ujung bebas dan beban merata diberikan dalam tabel di bawah ini. ^[6]

Distribusi	Max. nilai
Kantilever balok dengan beban akhir
$M (x) = P (x - L)$	$M A = P L$
$Q (x) = P$	$Q max = P$
$w (x) = \ tfrac {Px ^ 2 (3L-x)} {} 6EI$	$w_C = \ {tfrac PL ^ 3} {} 3EI$
Kantilever balok dengan beban terdistribusi secara merata
$M (x) = - \ tfrac {q (L ^ 2-2Lx + x ^ 2)} {2}$	$M_A = \ {tfrac QL ^ 2} {2}$
$Q (x) = q (L - x),$	$Q A = L q$
$w (x) = \ {tfrac qx ^ 2 (^ 2-6L 4Lx + x ^ 2)} {} 24EI$	$w_C = \ {tfrac QL ^ 4} {} 8EI$

Solusi untuk beberapa konfigurasi biasa ditemui lainnya sudah tersedia dalam buku pelajaran tentang mekanika bahan dan teknik buku pegangan.

[ sunting ]balok statis tak tentu

Para momen lentur dan gaya geser dalam Euler-Bernoulli balok sering dapat ditentukan langsung menggunakan keseimbangan statiskekuatan dan momen . Namun, untuk kondisi batas tertentu, jumlah reaksi dapat melebihi jumlah persamaan keseimbangan independen. ^[6]seperti ini disebut balok statis tak tentu .

Built-in balok yang ditunjukkan pada gambar di bawah ini adalah statis tak tentu. Untuk menentukan tegangan dan defleksi balok seperti, metode yang paling langsung adalah untuk memecahkan persamaan Euler-Bernoulli balok dengan kondisi batas yang sesuai. Tapi solusi analitis langsung dari persamaan berkas yang mungkin hanya untuk kasus-kasus yang paling sederhana. Oleh karena itu, teknik tambahan seperti superposisi linear sering digunakan untuk memecahkan masalah balok statis tak tentu.

Metode superposisi melibatkan penambahan solusi dari sejumlah masalah statis tentu yang dipilih sedemikian rupa sehingga kondisi batas untuk jumlah permasalahan individu menambahkan hingga mereka dari masalah asli.

(A) merata didistribusikan q beban.	(B) didistribusikan beban linear dengan ₀ q maksimum
$M_ {\ mathrm {max}} = \ {cfrac QL ^ 2} {12} ~; ~ ~ W_ {\ mathrm {max}} = \ {cfrac QL ^ 4} {} 384EI$
(C) P Konsentrat beban	(D) Momen M ₀

Masalah lain yang biasa ditemui balok statis tak tentu adalah balok kantilever dengan ujung bebas didukung pada roller. ^[6] Saat-saat lentur, gaya geser, dan defleksi balok seperti tercantum di bawah ini.

Distribusi	Max. nilai
$M (x) = - \ tfrac {q} {8} (L ^ 2-5Lx +4 x ^ 2)$	$\ Begin {align} M_B & = - \ tfrac {9qL ^ 2} {128} \ mbox {at} x = \ {tfrac 5L} {8} \ \ & = M_A \ ql tfrac {^ 2} {8} \ end {align}$
$Q (x) = - \ tfrac {q} {8} (8x-5L)$	$Q_A = - \ tfrac {5QL} {8}$
$w (x) = \ {tfrac qx ^ 2} {} 48EI (3L ^ 2-5Lx +2 x ^ 2)$	$W_ {\ mathrm {max}} = \ {tfrac QL ^ 4} {185EI} \ mbox {at} x = 0.5785L$

[ sunting ]Ekstensi

Asumsi kinematik yang di atasnya Euler-Bernoulli balok teori didirikan memungkinkan untuk diperluas untuk analisis yang lebih maju.Superposisi sederhana memungkinkan untuk tiga dimensi beban transversal. Menggunakan alternatif persamaan konstitutif dapat memungkinkan untuk viskoelastik atau plastik deformasi balok. Euler-Bernoulli teori balok juga dapat diperluas untuk analisis balok melengkung, tekuk balok , balok komposit, dan lendutan balok geometris nonlinier.

Euler-Bernoulli teori balok tidak menjelaskan efek melintang geser saring. Akibatnya itu underpredicts lendutan dan overpredicts frekuensi alami. Untuk balok tipis (balok panjang rasio ketebalan urutan 20 atau lebih) efek-efek ini kurang penting. Untuk balok kental, namun, efek ini bisa signifikan. Teori balok lebih maju seperti teori balok Timoshenko (dikembangkan oleh ilmuwan kelahiran Rusia Stephen Timoshenko ) telah dikembangkan untuk memperhitungkan efek ini.

[ sunting ]defleksi Besar

Euler-Bernoulli balok

Teori Bernoulli Euler-asli hanya berlaku untuk strain yang sangat kecil dan rotasi kecil. Teori ini dapat diperpanjang dengan cara yang mudah untuk masalah yang melibatkan rotasi cukup besar asalkan ketegangan tetap kecil dengan menggunakan von Kármánstrain. ^[7]

Euler-Bernoulli hipotesa bahwa bagian tetap pesawat pesawat dan normal terhadap sumbu memimpin balok untuk perpindahan dari bentuk

$v_1 = v_0 (x) - z \ cfrac {} {dx dw_0} ~; ~ ~ ~ v_2 = 0; ~ ~ v_3 = w_0 (x)$

Menggunakan definisi dari strain Hijau Lagrangian dari teori finite strain , kita dapat menemukan strain von Karman untuk balok yang berlaku untuk rotasi besar tetapi strain kecil. Strain ini memiliki bentuk

$\ Begin {menyelaraskan} \ varepsilon_ {11} & = \ {cfrac du_0} {} dx_1 - x_3 \ {d ^ cfrac 2w_0} {dx_1 ^ 2} + \ frac {1} {2} \ left [\ left (\ cfrac {du_0} {} dx_1-x_3 \ cfrac {d} {^ 2w_0 dx_1 ^ 2} \ right) ^ 2 + \ left (\ cfrac {} {dw_0 dx_1} \ right) ^ 2 \ right] \ \ \ varepsilon_ {22} & = 0 \ \ \ {33} varepsilon_ & = \ frac {1} {2} \ left (\ cfrac {} {dw_0 dx_1} \ right) ^ 2 \ \ \ varepsilon_ {23} & = 0 \ \ \ {31} varepsilon_ & = \ frac {1} {2} \ left (\ cfrac {} {dw_0 dx_1} - \ cfrac {} {dw_0 dx_1} \ right) - \ frac {1} {2} \ left [\ left (\ cfrac {du_0} {} dx_1-x_3 \ {d ^ cfrac 2w_0} {dx_1 ^ 2} \ right) \ left (\ cfrac {} {dw_0 dx_1} \ right) \ right] \ \ \ varepsilon_ {12} & = 0 \ end {menyelaraskan}$

Dari prinsip kerja virtual , keseimbangan kekuatan dan momen pada balok memberikan kita persamaan kesetimbangan

$\ Begin {align} \ {cfrac dN_ {xx}} {dx} + f (x) & = 0 \ \ \ cfrac {d ^ 2M_ {xx}} {dx} ^ 2 + q (x) + \ {cfrac d} {dx} \ left ({N_ xx} \ cfrac {} {dx dw_0} \ right) & = 0 \ end {align}$

dimana

f (x)

adalah beban aksial,

q (x)

adalah beban transversal, dan

$N_ {xx} = \ int_A \ sigma_ {xx} ~ dA ~; ~ ~ M_ {xx} = \ int_A z \ sigma_ {xx} ~ dA$

Untuk menutup sistem persamaan kita membutuhkan persamaan konstitutif yang berhubungan stres terhadap regangan (dan karenanya menekankan untuk pemindahan). Untuk rotasi besar dan kecil strain hubungan ini

$\ Begin {align} N_ {xx} & = A_ {xx} \ left [\ cfrac {} {dx du_0} + \ frac {1} {2} \ left (\ cfrac {} {dx dw_0} \ right) ^ 2 \ right] - B_ {xx} \ {d ^ cfrac 2w_0} {dx ^ 2} \ \ M_ {xx} & = B_ {xx} \ left [\ cfrac {} {dx du_0} + \ frac {1} {2} \ left (\ cfrac {} {dx dw_0} \ right) ^ 2 \ right] - D_ {xx} \ cfrac {d ^ 2w_0} {dx ^ 2} \ end {align}$

dimana

$A_ {xx} = \ int_A E ~ dA ~; ~ ~ B_ {xx} = \ int_A ze ~ dA ~; ~ ~ D_ {xx} = \ int_A z ^ 2E ~ dA ~.$

Jumlah

A x x

adalah kekakuan ekstensional ,

B x x

adalah kekakuan ekstensional-bending digabungkan, dan

D x x

adalah kekakuan lentur.

Untuk situasi di mana balok memiliki seragam penampang dan tidak ada beban aksial, persamaan yang mengatur untuk rotasi besar-Euler-Bernoulli balok adalah

$EI ~ \ cfrac {\ mathrm {d} ^ 4 w} {\ mathrm {d} x ^ 4} - \ frac {3} {2} ~ EA ~ \ left (\ cfrac {\ mathrm {d}} {w \ mathrm {d} x} \ right) ^ 2 \ left (\ cfrac {\ mathrm {d} ^ 2 w} {\ mathrm {d} x ^ 2} \ right) = q (x)$

[ sunting ]Lihat juga

Terapan mekanika
Pembengkokan
Tekuk
Lentur kekakuan
Lempeng teori
Sandwich teori
Singularity fungsi
Strain (ilmu material)
Teorema dari tiga momen (Teorema Clapeyron ini)
Three point flexural test

[ sunting ]Catatan

^ Timoshenko, S., (1953), Sejarah kekuatan bahan, McGraw-Hill New York
^ Truesdell, C., (1960), Mekanisme rasional badan fleksibel atau elastis 1638-1788, Venditioni Exponunt Orell Fussli Turici.
^ Ballarini, Roberto (18 April, 2003). "The Da Vinci-Euler-Bernoulli Beam Teori?" Teknik Mesin. Majalah . Diperoleh 2006/07/22.
^ Seon M. Han, Haym Benaroya dan Timotius Wei (22 Maret 1999) (PDF). Dinamika melintang getar Balok menggunakan empat Teori Teknik . akhir versi. Academic . Diperoleh 2007/04/15.
^ McKenzie, William (2006). Contoh dalam Analisis Struktural. Taylor & Francis.
^ ^{a b c d e f g h} Gere, JM dan Timoshenko, SP, 1997, Mekanika Bahan, PWS Publishing Company.
^ Reddy, JN, (2007), analisis elemen hingga nonlinier, Oxford University Press.

[ sunting ]Referensi

EA Witmer (1991-1992). "Dasar Bernoulli Euler Beam-Teori". Catatan MIT Teknik Kursus Bersatu. hal 5-114 untuk 5-164.

Selasa, 21 Februari 2012